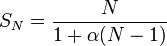Hukum Amdahl (Pemrograman Parallel)

Pemrograman Paralel

Pemrograman paralel adalah teknik pemrograman komputer yang memungkinkan eksekusi perintah/operasi secara bersamaan (komputasi paralel), baik dalam komputer dengan satu (prosesor tunggal) ataupun banyak (prosesor ganda dengan mesin paralel) CPU. Bila komputer yang digunakan secara bersamaan tersebut dilakukan oleh komputer-komputer terpisah yang terhubung dalam suatu jaringan komputer lebih sering istilah yang digunakan adalah sistem terdistribusi (distributed computing).

Motivasi

Tujuan utama dari pemrograman paralel adalah untuk meningkatkan performa komputasi. Semakin banyak hal yang bisa dilakukan secara bersamaan (dalam waktu yang sama), semakin banyak pekerjaan yang bisa diselesaikan. Analogi yang paling gampang adalah, bila anda dapat merebus air sambil memotong-motong bawang saat anda akan memasak, waktu yang anda butuhkan akan lebih sedikit dibandingkan bila anda mengerjakan hal tersebut secara berurutan (serial). Atau waktu yg anda butuhkan memotong bawang akan lebih sedikit jika anda kerjakan berdua.
Performa dalam pemrograman paralel diukur dari berapa banyak peningkatan kecepatan (speed up) yang diperoleh dalam menggunakan tehnik paralel. Secara informal, bila anda memotong bawang sendirian membutuhkan waktu 1 jam dan dengan bantuan teman, berdua anda bisa melakukannya dalam 1/2 jam maka anda memperoleh peningkatan kecepatan sebanyak 2 kali.

Peningkatan Kecepatan

Peningkatan kecepatan dapat diformulasikan dalam persamaan berikut ini

Dimana T₁ adalah waktu yang dibutuhkan untuk menyelesaikan pekerjaan (program komputer) bila dijalankan dalam satu komputer. Dan T_j adalah waktu yang dibutuhkan jika pekerjaan dikerjakan bersamaan oleh beberapa komputer.
Ada limitasi dalam usaha membuat suatu program komputer berjalan lebih efisien melalui peningkatan kecepatan, hukum yang menetapkan batasan ini dikenal sebagai Hukum Amdahl. Ide dari hukum amdahl ini adalah bahwa anda hanya akan bisa meningkatkan efisiensi program komputer anda, sebatas pada bagian tertentu dari program tersebut yang dapat di paralelkan. Sementara bagian yang memang harus dilaksanakan secara berurutan, akan menjadi penentu performa akhir.
Kembali ke analogi memasak tadi, bila anda harus menggunakan sarung tangan sebelum menyalakan kompor ataupun memotong bawang, maka waktu yang anda butuhkan untuk memakai sarung tangan ini adalah waktu serial, yang tidak dapat dihindari. Sementara waktu untuk memasak dan memotong bawang tadi adalah bagian yang bisa diparalelkan.

Hukum Amdahl

Telah dijelaskan bahwa dari T₁ (waktu yg dibutuhkan menjalankan pekerjaan dalam satu komputer) tadi, ada sebagian yg tidak bisa diparalelkan. Untuk menyatakan ini kita gunakan notasi α dimana menunjukkan berapa bagian dari T₁ yang tidak bisa dijadikan paralel (atau bagian serial dari program ini).
Maka kita ketahui α * T₁ adalah waktu yg tidak akan terpengaruh oleh bertambahnya komputer yg digunakan (a).
Sisanya (1 − α) * T₁ adalah waktu yang akan berkurang menjadi bila kita menggunakan N komputer tambahan {b) .
Sehingga waktu total yang dibutuhkan untuk menjalankan pekerjaan dalam N komputer adalah (a) + (b) alias :

Peningkatan kecepatan yang kita peroleh dari persamaan ini adalah :

Mungkin anda akan mendapati persamaan speed up yang terlihat berbeda tapi pada dasarnya sama. Persamaan dibawah, bisa didapat dari persamaan diatas, dengan mengeliminasi komponen T₁ (pada bagian atas dan bawah persamaan), lalu mengatur N dan α

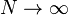Bila anda cermati persamaan di atas, bisa dilihat bahwa jika kita menggunakan komputer yang amat banyak () komponen (b) akan dapat diabaikan, menyisakan persamaan :

Inilah batas maksimum peningkatan kecepatan yang bisa dicapai menurut hukum Amdahl yaitu perbandingan terbalik dari seberapa banyak bagian serial dari suatu pekerjaan.
Dalam sistem terdistribusi dimana anda berusaha menggunakan lebih banyak prosesor untuk menyelesaikan masalah, akan ada imbal balik. Menggunakan komputer tambahan dari lokasi yang berbeda memberikan anda sumber komputasi baru, tapi juga melibatkan biaya komunikasi tambahan, saat anda harus memberikan pekerjaan tersebut pada komputer yg terpisah.


 KESIMPULAN

Pemrograman parallel memungkinkan eksekusi perintah/operasi secara bersamaan. Peningkatan kecepatan dapat diformulasikan dalam persamaan berikut ini


Hukum Amdahl berperan dalam menetapkan batasan limitasi dalam usaha membuat suatu program komputer berjalan lebih efisien melalui peningkatan kecepatan. Berisikan bahwa peningkatan efisiensi program komputer sebatas pada bagian tertentu dari program yang dapat di paralelkan, sedangkan bagian yang memang harus dilaksanakan secara berurutan, akan menjadi penentu performa akhir.
Jika kita menggunakan komputer yang amat banyak (N → ∞ ) komponen (b) akan dapat diabaikan, menyisakan persamaan :

Batas maksimum peningkatan kecepatan yang mampu dicapai menurut hukum Amdahl yaitu perbandingan terbalik dari seberapa banyak bagian serial dari suatu pekerjaan.

Sumber : http://id.wikipedia.org/wiki/Komputasi_paralel

Read More......